
I noticed, students were able to clarify misconceptions and connect ideas via the visualization of this activity, in general, the learning process was enhanced. Active learning was applied in this activity, via questioning, discussion, and review of the topic: The Domain and Range of a Function.
#COMPOSITE FUNCTIONS DESMOS ACTIVITY CODE#
Go to and use the code 68E VUK Note: Before working on this assignment, it may also. As students went through the activity, the answers posted were shared, this allowed students to make sure they were in the right track, I provided help and hints when students needed it. This activity is designed for the students to discover the relationship between the transformtions of a graph and the parameters of the function of the graph. Complete the Desmos Activity Compositions of Functions. This DESMOS activity was not graded, and served to help my students understand and master the idea of Domain and Range of a Function associated to the graph of the Function, via vertical and horizontal strips. Through out the activity I asked students “what if… ” questions to help them figure out the answers reasoning.ġ6 students participated, this activity took 30 minutes. the “interactive visualization” of this DESMOS activity, in my opinion, brings clarity and helps students “make sense” of what is explained in class.

“mistakes are part of the learning process” I often said to encourage students to finish with the activity. This time, students were able to check if what they posted was right or wrong as well as what their classmates were posting, this helped them, in most cases, to understand the nature of their mistakes, correct them and post again. It can be used as an introduction to Hyperbolas.
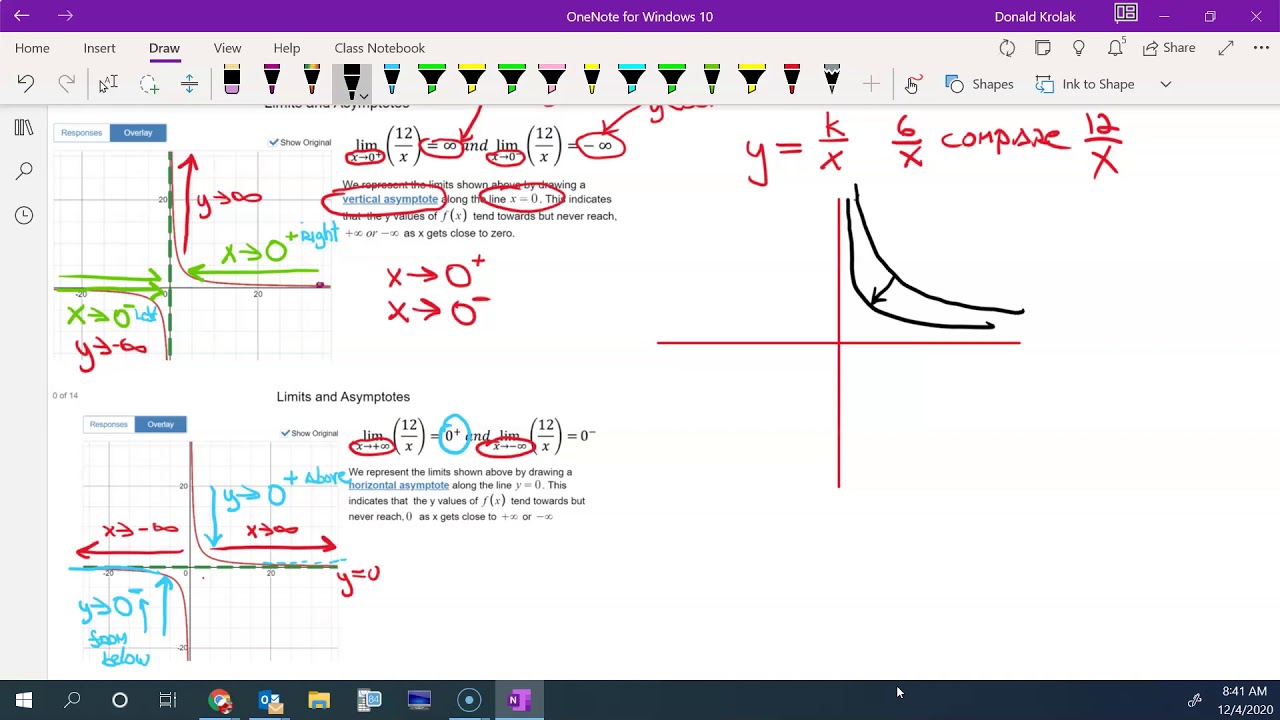

As I walked around helping students, I noticed that the counterintuitive nature of “horizontal shifts” was better understood thanks to the “visualization” of what they posting. This activity guides learners to discover why an equation would sometimes approach a line without ever touching or intersecting it. For all questions during the activity the function was expressed as f(x), which helped students to understand that these transformations can be applied to any function whatsoever. In this DESMOS activity students were able to visualize how, in general, the graph of function changes, under rigid and none-rigid transformations. 12 students participated, this activity took 30 minutes.


 0 kommentar(er)
0 kommentar(er)
